摘要:本文对丝状菌污泥膨胀现象进行分析和综合,并在广义的Monod方程的基础上,提出了统一的污泥膨胀理论。该模型可以很好的解释基质限制、溶解氧限制、营养物缺乏型,高、低pH和硫化氢因素引起的五种类型主要活性污泥丝状菌膨胀。这包括了大部分的污泥膨胀现象。利用广义的Monod方程采用双基质限制(碳源和溶解氧)模型和系统动力学方程进行了计算机模拟研究。对负荷与溶解氧,水质和水量变化等因素对于菌胶团细菌和丝状菌的竞争关系的影响进行了深入的研究,并在此基础上对于不同的膨胀类型对应提出了对应的控制策略。
关键词:污泥膨胀 丝状菌 菌胶团菌 广义Monod方程
一、污泥膨胀控制方法的演化过程
早期控制丝状菌引起的污泥膨胀(简称污泥膨胀)的主要手段是利用丝状菌具有较大的比表面积值,采用药剂杀死丝状菌,或是投加无机或有机混凝剂或助凝剂以增加污泥絮体的比重<1>。这些方法往往无法彻底解决污泥膨胀问题,并且相反地会带来出水水质恶化的不良后果。人们逐渐认识到活性污泥中的菌胶团细菌和丝状菌形成一个共生的微生物生态体系。在这种共生关系中,丝状微生物是不可缺少的重要微生物,其在活性污泥工艺中对于高效、稳定地净化污水起重要作用。人们逐渐的从简单地杀死丝状菌过渡到利用曝气池中的生长环境,调整丝状菌的比例,控制污泥膨胀的发生--即环境调控阶段。环境调控概念的使用是人们在污泥膨胀控制技术和实践上的一大进步。其主要出发点是使曝气池中的生态环境,有利于选择性地发展菌胶团细菌,应用生物竞争的机制抑制丝状菌的过度生长和繁殖,将丝状菌控制在一个合理的范围之内,从而控制污泥膨胀的发生和发展。同时利用丝状菌特性净化污水,稳定处理工艺。近年选择器理论得到充分发展和应用就是这一概念具体体现<2><3>。
二、统一的污泥膨胀的理论
由于活性污泥是一混合培养系统,活性污泥是菌胶团细菌与丝状菌的共生系统,任何活性污泥系统中都存在着丝状茵。丝状菌也不仅仅是一种菌存在,活性污泥中存在着至少30种可能引起污泥膨胀的丝状菌,污泥膨胀的原因是复杂的。在丝状茵与菌胶团细菌平衡生长时,不会产生膨胀问题。只有当丝状茵生长超过菌胶团细菌时,就会出现膨胀问题。污泥膨胀是由丝状茵和菌胶团细菌生理和生化性质不同所决定的,这两类细菌性质的差异见表1。
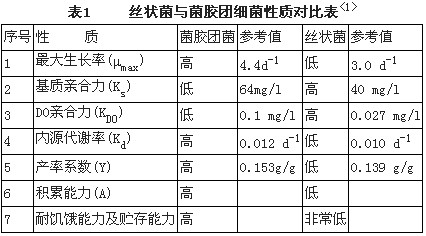 |
通过对近年来活性污泥膨胀问题国内外研究进展的分析和综合,可以将主要的活性污泥丝状菌膨胀的原因分为五种类型:即a)基质限制;b)溶解氧限制;c)营养物缺乏型高;d)高、低pH引起; e) 和硫化氢因素等膨胀类型<4>。
1. 广义的Monod方程
丝状菌与菌胶团细菌竞争的数学模型,其遵循多种基质限制的广义Monod方程,即Monod-McGee方程<1>:
μ=μmax[S1/(K1+S1)][S2/(K2+S2)]…[Sn/(Kn+Sn)] (1)
其中:μmax:最大生长速率(d-1);Ki:第I种基质亲和力(mg/l);Si:第I种基质。
根据动力学方程(1)可知,基质限制、溶解氧限制和营养物缺乏型的膨胀问题都可用广义Monod方程来加以解释。值得说明的是当氮严重缺乏时并不能归入这一理论。原因在于由于缺乏氮,使微生物不能充分利用碳源合成细胞物质,使得过量的碳源被转变为多糖类胞外贮存物,这种贮存物是高度亲水型化合物,从而形成结合水,影响污泥沉降性能,产生了高粘度性的膨胀,其类型不属于丝状菌膨胀<5>。
2. 硫化氢的等其他类型的问题
关于pH的影响,可在动力学方程的参数上,作为动力学常数的乘积因子的形式进行耦合,或者单独列出其动力学方程,从而统一在广义Monod方程之下。关于H2S的影响,从文献中报道引起污泥膨胀的H2S数值很低,一般是在1~2.0mg/l<5>。笔者认为每升几毫克硫化氢似乎不足以供发硫菌或贝氏硫细菌大量增值的能量,相反几十到上百ppm的有机酸是值得注意的因素。我们进行了向污水中添加H2S的实验,通过实验发现即使H2S浓度达到 50mg/l也并不发生膨胀<6>。事实上,一些厌氧装置运转的较好,虽然出水含有大量H2S,但是挥发酸浓度很低时,好氧后处理也不发生膨胀。当污水处于腐败和厌氧条件时,污水厌氧发酵的同时产生H2S和挥发酸。挥发酸主要包括乙酸、丙酸等,这些低分子易于降解,造成耗氧速率的增加<7>,从而引起氧的限制型膨胀,这是造成污泥膨胀的根本原因。而H2S的出现是污水厌氧发酵的一个伴随现象。因此H2S的膨胀类型可归为溶解氧限制类型的膨胀,从而广义的Monod动力学模型可以在一定程度上很好地统一污泥膨胀的理论。
3. 双基质的Monod方程
由于城市污水中N、P和其它营养元素一般不缺乏,因此在一般情况下,可只考虑碳源限制和DO限制两种情况。这样城市污水的丝状菌膨胀问题就简化为两种主要类型的膨胀问题,即基质限制和溶解氧限制类型。
μ=μmax [S/(Ks+S)][DO/KDO+DO] (2)
其中:μmax:最大生长速率(d-1);Ks:基质亲和力(mg/l);KDO=溶解氧亲和力(mg/l);
三、污泥膨胀数学模型的研究
1、污泥膨胀的数学模型
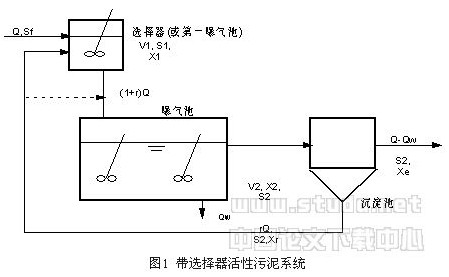 |
为了简化系统模型,数学模型的建立基于以下几个假设:1)活性污泥由两大数群微生物组成,即丝状菌和菌胶团菌;2)微生物生长主要受到碳源和DO限制;3)微生物生长的动力学可用同一基本模型来描述;4)曝气池是完全混合式;模型所描述的系统如图1所示。其中反应器1根据不同的实验目的,分别可以是选择器、曝气池等等,反应器2是曝气池。在没有选择器的系统中,回流污泥按虚线所示的途径回流。根据以上假设及图1中的物料平衡关系,可给出选择器和曝气池中基质(碳源和DO)和微生物(菌胶团和丝状菌)的如下一组方程:
对选择器有如下方程成立:
对菌胶团菌: dX11/dt = (μ1-kd1-1/θc) X11 (3)
对丝状菌:dX21/dt = (μ2-kd2-1/θc) X21 (4)
对碳源基质:dS11/dt == Dk(S10+rS12)-(1+r)D1S11-μ1X11/Y1-μ2X21/Y2 (5)
对溶解氧: dS21/dt = -(1+r)D1S21 +Kla(S2S-S21) -μ1X11/Y1-μ2X21/Y2 (6)
对曝气池有如下方程成立:
对菌胶团菌:dX12/dt = (1+r)D2(X11-X12)+(μ1-kd1) X12 (7)
对丝状菌: dX22/dt = (1+r)D2(X21-X22)+(μ1-kd1) X22 (8)
对碳源基质:dX12/dt = (1+r)D2(S11-S12)-μ1X12/Y1-μ2X22/Y2 (9)
对溶解氧: dS22/dt = (1+r)D2(S21-S22)+Kla(S2s-S22) -μ1X12/Y1-μ2X22/Y2 (10)
其中: 状态变量:Xik=污泥浓度(mg/l);Sjk=基质浓度(mg/l),i=1,2分别代表菌胶团和丝状菌;
j=1,2分别代表碳源和DO;S10=碳源基质初始浓度(mg/l); S2s=饱和溶解氧浓度(mg/l);
操作变量:Dk=稀释率(d-1) k=1,2分别代表选择器和曝气池; r=回流比;
动力学常数:kdi衰减常数(d-1);Yi=产率系数(g/g);Kla=传质系数(min-1);其常数见表1;
μi= 比生长速率采用的双基质模型(方程2),i=1,2分别代表菌胶团和丝状菌;
2. 曝气强度和负荷的影响
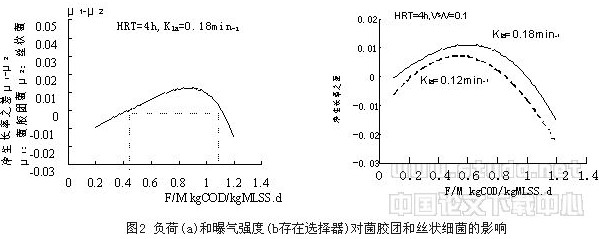 |
图2是根据方程(3-10)的计算机模拟结果。从图2a可见丝状菌和菌胶团细菌的竞争优势是根据负荷而变化的。根据负荷的不同,可划分为三个不同阶段:低负荷阶段(<0.4kg COD/kgMLSS.d)这时溶解氧的供应是充分的出现基质限制的情况。高负荷阶段(>1.1kg COD/kgMLSS.d)由于主体溶液中的基质浓度比较高,出现溶解氧限制的情况。在这之间是中等负荷范围,在这一范围丝状菌与絮状菌处于合理的比例,系统不发生膨胀。以上结果解释了为什么在高、低负荷下都会发生污泥膨胀的原因。
图2b是在有选择器条件下,不同曝气条件下(Kla)计算机模拟结果。上述的模拟结果同样表明即使在存在选择器的情况下,在低负荷和高负荷范围仍然会发生膨胀。膨胀的界限值与没有选择器的系统不同,对于完全混合曝气池界上、下限下移。对于高负荷系统高的曝气强度可以提高污泥膨胀发生的上限,但同样较低了低负荷系统发生膨胀的下限。从图2b可见对于中等负荷阶段如果供氧不充分,丝状菌仍有可能大量繁殖并形成膨胀。对于不同的曝气强度,两种微生物竞争优势发生转变的界限值是不同的。对于这就是双基质动力学方程与传统的单独碳源基质限制动力学方程描述膨胀现象的本质区别。实验的结果也表明,完全混合曝气池对不同负荷下,维持稳定的沉降性能,所需要的溶解氧浓度是不一样的。而不是象文献报道维持在固定的1.0~2.0mg/l之间<1>。这解释了国内外众多研究中,对于溶解氧对污泥膨胀的影响报道十分不一致的原因。提高供氧能力的方法,一是增加供风量,二是用充氧能力强的装置。
3. 流量和浓度变化的影响
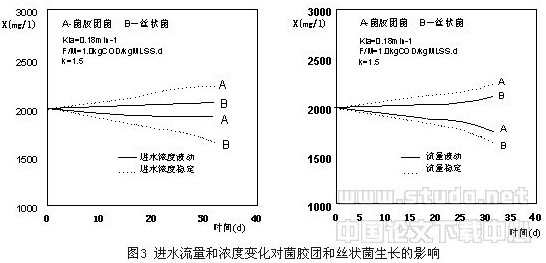
实际的污水处理厂负荷是变化的,实验发现在停留时间3、4和5h.下,系统的溶解氧浓度分别为1.2,2.2和3.0mg/l。图3是流量和基质增加幅度为1.5倍采用计算机模拟结果。在稳定的流量和浓度条件下,长期运行是菌胶团细菌占优势。流量或是基质浓度的变化会造成丝状菌的过度生长,而丝状菌的生长不是一简单的可逆过程,结果会造成了污泥沉降性能的变化。值得说明的是上述结果是在相对高的负荷下的模拟结果,研究表明对低负荷结果相反。
 |
四、讨论和结论
1) 通过分析将丝状菌膨胀概括为5种类型,即:低基质浓度、低溶解氧、营养物(N、P)缺乏型、高H2S浓度和高、低pH引起的膨胀。采用广义Monod方程可解释大部分类型的膨胀问题,这在一定程度上统一了污泥膨胀理论。由于城市污水中N、P和其它营养元素一般不缺乏,因此在一般情况下,只考虑碳源限制和DO限制两种情况;
2) 在双基质限制下,低负荷的完全混合曝气池不利于污泥沉淀性能的改善,而中、高负荷的膨胀则在完全混合曝气池中有所缓解。中、高负荷系统由于首端缺氧不利污泥沉降性能,所以在推流式曝气池需要采取措施避免供氧不足。反之,推流式曝气池有利于克服低负荷的膨胀,即高负荷与低负荷是两种类型完全相反的膨胀现象。
3) 对活性污泥膨胀,既要从宏观角度考虑,又要从微观角度考虑,而宏观与微观是相对的。就活性污泥工艺的运转条件而言,负荷、基质浓度和溶解氧浓度的水平是宏观条件。但曝气池首端的实际的负荷、基质浓度和溶解氧浓度是更为重要的因素。后者是决定污泥膨胀的微环境,种群的动态是由其微环境中的营养物的条件所确定的;
4) 传统的选择器类型是仅仅考虑低基质浓度型膨胀。选择器是在完全混合或推流曝气池前加一个停留时间非常短(15min.)的小池,在选择器内利用两类细菌不同的生长速率选择性地培养和发展菌胶团细菌,使其成为曝气池中的优势菌。在以上的理论分析和研究的基础上,可以对选择器的概念进行扩展。广义的选择器可以包括低溶解氧型膨胀。可采用不同的选择器的形式,如再生池和强化曝气池等方法,恢复菌胶团细菌的降解能力、提高供氧能力和降低负荷来控制高负荷型的污泥膨胀。
参考文献
1) 王凯军(1993),活性污泥膨胀机理与控制,中国环境出版社
2) Antonia O. Lau, Peter F. Strom and David Jenkins (1984),The Competitive Growth of Floc-forming and Filamentous Bacteria: a Model for Activated Sludge Bulking, Journal WPCF, Vol.56, No.1, pp.24
3) J. Chudoba et al(1985) Control of Activity Sludge Filamentous Bulking: Experimental Verification of a Kinetic Selection Theroy, Water Res., Vol.19,No.2, pp. 567
4) 王凯军(1992),丝状菌型污泥膨胀的统一理论,环境科学,第13卷,第3期,pp.76
5) 田口 广(1982),活性污泥膨胀与控制对策, 孙玉修等译 中国建筑工业出版社
6) 齐吉山(1992),活性污泥膨胀的机理与控制,北京市环境保护研究所,硕士论文
7) 王凯军(1992),厌氧(水解)处理低浓度污水,中国环境出版社
作者: 王凯军,许晓鸣
