基于输出观测器的污水COD软测量方法

　　申请日2013.08.20

　　公开(公告)日2013.11.20

　　IPC分类号G01N33/18

　　摘要

　　一种基于输出观测器的污水COD软测量方法，它涉及一种污水COD软测量方法。本发明要解决污水处理过程中反应过程复杂、非线性关系强、部分关键变量难于测量的问题。该方法是将待测变量作为系统输出，构建性能良好的输出观测器，其中的观测器参数由历史测量数据离线辨识得到。本发明的主要优点有：1)不依赖于对污水处理反应模型的先验知识，仅利用污水处理系统历史测量数据;2)基于成熟的控制理论，构建闭环观测器，动态性能优异，软测量效果好;3)应用范围广泛，除污水处理系统出水COD外，改进的系统应用于测量其他水质指标以及化工、冶炼、造纸等类似工业过程的产品成分。本方法应用于污水在线测量领域。

　　权利要求书

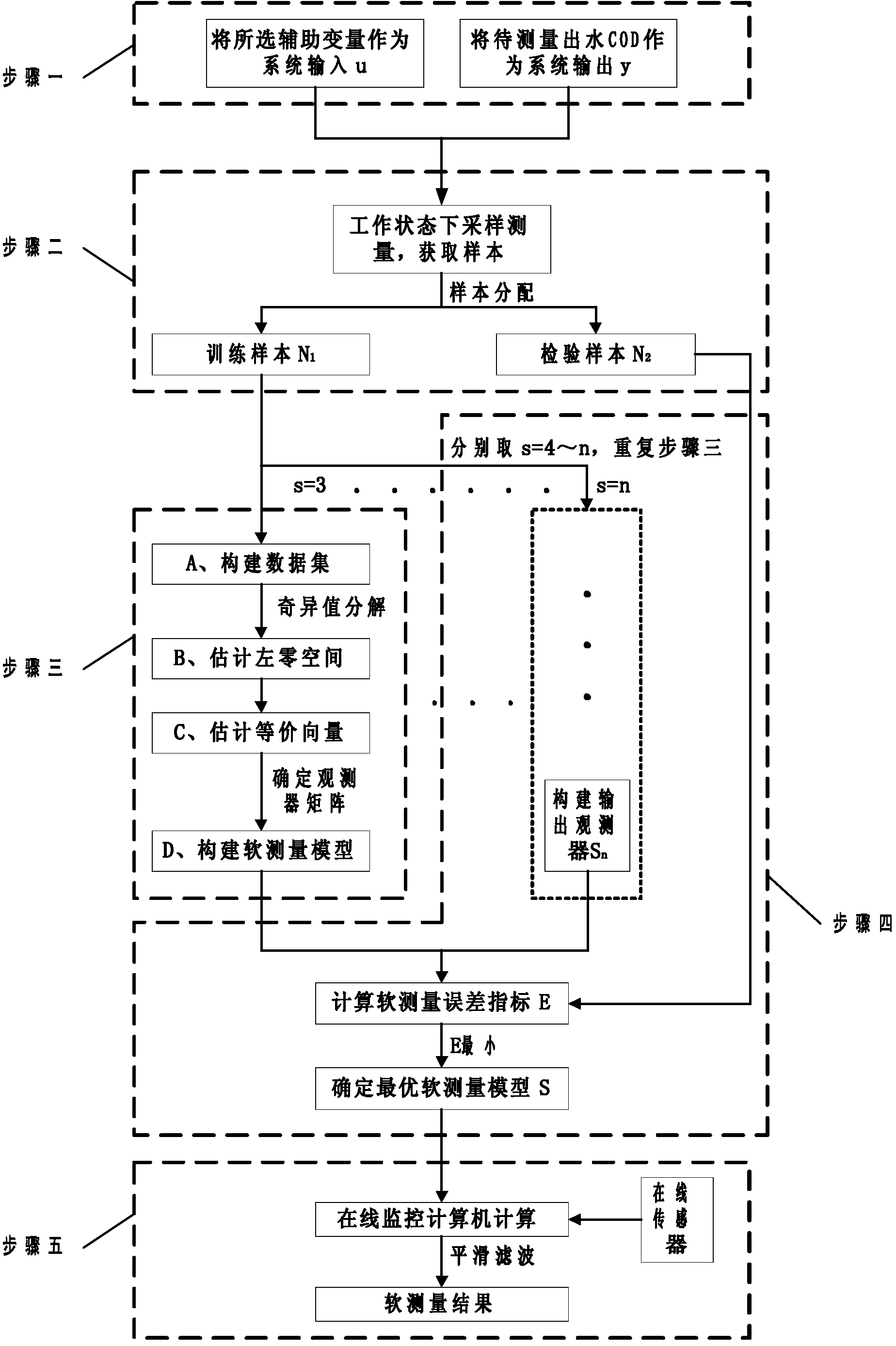
　　1.一种基于输出观测器的污水COD软测量方法，其特征在于所述的基于输出观测器的污水COD软测量方法是按照以下步骤进行的：

　　步骤一，选择辅助变量和待测变量：选取TOC、DO、ORP、pH、T、HRT和r作为辅助变量，分别设为u1,…,u7，将出水COD设为y，所述的y为待测变量;将污水处理过程定义为反应系统，系统输入为u=[u1…u7]∈Rl，l=7，系统输出y∈Rm，m=1; 其中，TOC为进水总有机碳含量，DO为反应池溶解氧，ORP为氧化还原电位，pH为酸碱度， T为水温，HRT为水力停留时间，r为回流比;

　　步骤二，数据采集：利用传感器采集污水的辅助变量和待测变量的数据样本，其中，辅助变量数据样本为u1(i),…,u7(i)，待测变量数据样本为y(i);i=1,…,N0，N0为采样数量，传感器采集数据样本的时间为10s～10min;

　　取N1组数据样本为训练样本，取N2数据样本为检测样本，其中，N1与N2均为正整数， N1+N2=N0;

　　步骤三，构建软件测量模型：

　　A、构建数据集：

　　选取采集训练样本时间的中间时刻k，取训练样本N1中的数据，按如下方式构建数学矩阵Zp和Zf：

　　 $Z_{p} = [\begin{matrix} Y_{p} \\ U_{p} \end{matrix}],$ 其中， $Y_{p} = [\begin{matrix} Y (k - s) \\ . \\ . \\ . \\ Y (k - 1) \end{matrix}],$ $U_{p} = [\begin{matrix} U (k - s) \\ . \\ . \\ . \\ U (k - 1) \end{matrix}];$

　　 $Z_{f} = [\begin{matrix} Y_{f} \\ U_{f} \end{matrix}],$ 其中， $Y_{f} = [\begin{matrix} Y (k) \\ . \\ . \\ . \\ Y (k + s - 1) \end{matrix}],$ $U_{f} = [\begin{matrix} U (k) \\ . \\ . \\ . \\ U (k + s - 1) \end{matrix}];$

　　Y(j)=[y(j)…y(j+N-1)]，U(j)=[u(j)…u(j+N)]

　　其中，N为正整数，N1>N+2s，N≥s+1，所述的s=3;

　　B、估计左零空间：

　　计算并对其进行奇异值分解，结果如下：

　　 $\frac{1}{N} Z_{f} Z_{p}^{T} = U_{z} [\begin{matrix} Λ_{XY} & 0 \\ 0 & Λ_{Φ} \end{matrix}] V_{z}^{T},$

　　Uz=[Uz，XY Uz，res]，其中，ΛXY为对角阵，ΛΦ≈0;

　　C、估计等价向量，公式如下：

　　取的最后一行，记为β，β为等价向量;

　　满足：β=[βu βy]，

　　βu=[βu,0…βu,s]∈Rl(s+1)，

　　βy=[βy,0…βy,s]∈Rm(s+1)，βy,s=1;

　　D、构建软测量模型

　　构建系统的输出观测器，即为软测量模型sensors，其中软测量模型构建公式如下：

　　 ${sensor}_{s} : \{\begin{matrix} z_{s} (t + 1) = A_{s} z_{s} (t) + B_{s} u (t) + L_{s} \tilde{y} (t) \\ {\hat{y}}_{s} (t) = C_{s} z_{s} (t) + d_{s} u (t) \end{matrix}$

　　其中，u(t)为系统输入，为系统输出，zs(t)为内部变量，为软测量结果，

　　其中，系统的输出观测器参数确定方法如下：

　　 $B_{s} = - [\begin{matrix} β_{u, 0} \\ . \\ . \\ . \\ β_{u, s - 1} \end{matrix}] &Element; R^{s},$ cs=[0…0 1]∈Rs，ds=-βu,s， $L_{s} = - [\begin{matrix} β_{y, 0} \\ . \\ . \\ . \\ β_{y, s - 1} \end{matrix}];$

　　步骤四，确定最优观测器：

　　分别取s=4,…,l，重复步骤A至D，得l-3个软测量模型，根据s取值，各模型分别为sensor3,…,sensorl;将步骤一中的辅助变量数据样本u1(i),…,u7(i)和待测变量数据样本y(i)代入各软测量模型sensor3,…,sensorn中，得

　　定义评价指标其中y0(t)为测试样本中的实际输出结果;最优软测量模型S为E中数值结果最小的一组软测量模型;所述的最优软测量模型为 $S : \{\begin{matrix} z_{0} (t + 1) = A_{0} z_{0} (t) + B_{0} u (t) + L_{0} \tilde{y} (t) \\ {\hat{y}}_{0} (t) = C_{0} z_{0} (t) + d_{0} u (t) \end{matrix};$

　　步骤五，在线测量：

　　E、模型移植

　　将最优软测量模型S移植到在线监控计算机，实时获取的采样测量值u1,…,u7，以及计算出水COD值

　　F、在线滤波

　　通过在线滤波器对进行处理;处理公式如下：

　　 ${\hat{y}}_{f} (t) = a {\hat{y}}_{0} (k - 1) + (1 - a) {\hat{y}}_{0} (t),$

　　其中，α∈[0,1]为滤波因子。

　　2.根据权利要求1所述的一种基于输出观测器的污水COD软测量方法，其特征在于步骤D构建软测量模型中所述的

　　若有在线仪表，则为在线仪表读数，软测量结果为优化的测量数据;

　　若无在线仪表，则为离线采样获得的中值。

　　3.根据权利要求1所述的一种基于输出观测器的污水COD软测量方法，其特征在于步骤F在线滤波中所述的在线滤波器为平滑滤波器。

　　说明书

　　一种基于输出观测器的污水COD软测量方法

　　技术领域

　　本发明涉及一种污水COD软测量方法，特别涉及一种对污水处理系统出水COD的软测量方法。

　　背景技术

　　由于对出水水质、系统效率等指标要求的不断提高，在线、实时地对各项水质指标进行监测成为现代污水处理系统中必不可少的关键环节。对于温度、酸碱度等指标，通常采用在线测量仪表进行检测。然而，传统上采用的在线仪表存在诸多明显不足：1)易受干扰，存在较大的测量误差;2)时滞现象明显;3)部分水质变量无法在线测量;4)价格昂贵，维护费用高。相比之下，软测量技术能够很好的克服上述缺点，受到了普遍重视。

　　软测量技术主要是指，不依赖于在线传感器，而利用数学关系对在线可测量的数据进行处理，从而得到在线不可测的变量。通常，其主要步骤包括辅助变量的选择、数据采集与处理、软测量模型、在线校正等。经过多年的发展，人们已经提出了多种软测量技术，主要可分为两大类：1)依赖于模型的方法，入机理建模、状态估计;2)基于数据的方法，如：回归分析、人工神经网络、支持向量机等。前者通过对系统的分析，构建反应模型，来获得待测变量与可测变量间的关系。其主要优点在于理论成熟，测量效果好。但对于较为复杂的系统，建模过程困难甚至难以实现，从而限制了其使用范围。后者则主要通过历史数据训练得到合理的数学模型，并将其应用于在线测量，实用性更强。该类方法的不足在于对建模数据的数量和质量均有较高要求，并且对系统的变化不敏感，测量偏差较大。

　　发明内容

　　本发明的目的是为了解决污水处理过程中反应过程复杂、非线性关系强、部分关键变量难于测量的问题，而提供一种基于输出观测器的污水COD软测量方法。

　　本发明的一种基于输出观测器的污水COD软测量方法，是按照以下步骤进行的：

　　步骤一，选择辅助变量和待测变量：选取TOC、DO、ORP、pH、T、HRT和r作为辅助变量，分别设为u1,…,u7，将出水COD设为y，所述的y为待测变量;将污水处理过程定义为反应系统，系统输入为u=[u1 … u7]∈Rl，l=7，系统输出y∈Rm，m=1; 其中，TOC为进水总有机碳含量，DO为反应池溶解氧，ORP为氧化还原电位，pH为酸碱度， T为水温，HRT为水力停留时间，r为回流比;