您所在位置:首页>技术转移

基于多高斯核自优化相关向量机污水水质测量

　　申请日2015.06.16

　　公开(公告)日2015.09.16

　　IPC分类号G01N33/18

　　摘要

　　本发明公开了一种基于多高斯核自优化相关向量机的污水水质软测量方法，包括以下步骤：1)剔除污水输入和输出的数据中的异常点，由于各输入变量量纲的不同，对其进行归一化处理，归一化到[0,1]区间中;2)多高斯核函数相关向量机软测量模型模块;3)多高斯核函数核参数自优化算法;4)遗传优化算法对初始参数寻优模块;5)多高斯核函数自优化相关向量机软测量模型建模。本发明通过自优化方法确定各尺度上的核参数，运用遗传优化算法对初始参数寻优，建立最优模型，在保证模型收敛性和稀疏性的情况下，有效提高污水中BOD输出精度。

　　摘要附图

 

　　权利要求书

　　1.基于多高斯核自优化相关向量机的污水水质软测量方法，其特征在于， 包括以下步骤：

　　1)剔除污水输入和输出的数据中的异常点，由于各输入变量量纲的不同， 对其进行归一化处理，归一化到[0,1]区间中;

　　2)多高斯核函数相关向量机软测量模型模块，其计算公式：

　　给定一组输入和目标值xn∈RM，且考虑目标函数只 是一个标量，根据概率方程式，假设目标函数是模型的样本并且带有附加噪声：

　　tn=y(xn,w)+εn (1)

　　式中εn为附加噪声，服从(0,σ2)的高斯分布，且彼此间相互独立，因此 p(tn|y(xn),σ2)服从高斯分布，其分布由期望y(xn)和方差σ2决定，其中y(xn) 可由核函数的加权模型表示：

　　$y(x,w)=\underset{i=1}{\overset{N}{\Sigma }}{w}_{i}k(x,x_i)+w_0---\left(2\right)$

　　wi为模型权值，w=[w0,w1,w2,...,wn]T为(N+1)维列向量;k是核函数， φi=k(x,xi);t=[t1,t2,...tn]T为N维列向量，假设tn服从独立分布，数据集的 似然估计概率为：

　　$p\left(t\right|w,{\sigma }^2)={\left(2\pi {\sigma }^2\right)}^{-N/2}\exp \{-\frac{1}{2{\sigma }^2}{\left|\right|t-\mathrm{\Phi w}\left|\right|}^2\}---\left(3\right)$

　　φ(xn)=[1,k(xn,x1),k(xn,x2),...k(xn,xn)]T为(N+1)*1维矩阵，贝叶斯矩阵表示 为：Φ=[φ(x1),φ(x2),...,φ(xn)]T，其是N*(N+1)维;为了约束rvm模型中 权值w，假设其服从(0,αi-1)高斯分布，且设各权值间相互独立，其先验概率表 示如下：

　　$p\left(w\right|\alpha )=\underset{i=0}{\overset{N}{\Pi }}N\left(w_i\right|0,{{\alpha }_i}^{-1})---\left(4\right)$

　　α为N+1维超参数，引入超参数导致算法的稀疏性;

　　根据贝叶斯准则，可得到后验概率公式：

　　给定新的测试样本x，预测相应的目标t*，按照预测分布：

　　$p\left(t_{*}\right|t)=\∫p\left(t_{*}\right|w,\alpha ,{\sigma }^2)p(w,\alpha ,{\sigma }^2|t)d_w{d}_{\alpha }{d}_{{\sigma }^2}$

　　无法计算后验概率，因为无法计算$p\left(t\right)=\∫p\left(t\right|w,\alpha ,{\sigma }^2)p(w,\alpha ,{\sigma }^2)d_w{d}_{\alpha }{d}_{{\sigma }^2}$

　　所以将后验概率分解：p(w,α,σ2|t)=p(w|t,α,σ2)p(α,σ2|t)

　　可得权重的后验概率为：

　　$\begin{array}{c}p\left(w\right|t,\alpha ,{\sigma }^2)=\frac{p\left(t\right|w,{\sigma }^2)p\left(w\right|\alpha )}{p\left(t\right|\alpha ,{\sigma }^2)}\\ ={\left(2\pi \right)}^{-(N+1)/2}{\left|\Sigma \right|}^{-1/2}\exp \{-\frac{1}{2}{(w-u)}^T{\Sigma }^{-1}(w-u)\}\end{array}---\left(5\right)$

　　其后验协方差和均值分别为：

　　Σ=(σ-2ΦTΦ+A)-1 (6)

　　u=σ-2ΣΦTt (7)

　　因为p(α,σ2|t)∝p(t|α,σ2)p(α)p(σ2)，所以可以用后者等价前者：

　　$\begin{array}{c}p\left(t\right|a,{\sigma }^2)=\∫p\left(t\right|w,\beta )p\left(w\right|\alpha )d_w\\ ={\left(2\pi \right)}^{-N/2}{|{\sigma }^{2}I+\Phi A^{-1}{\Phi }^T|}^{-1/2}\exp (-\frac{1}{2}{t}^T\mathrm{Ct})\end{array}$

　　其中矩阵C=(σ2I+ΦA-1ΦT)-1，对上述式子取对数得：

　　$L=\log p\left(t\right|\alpha ,\beta )=-\frac{1}{2}(N\log \left(2\pi \right)+\log |C|+t^T{C}^{-1}t)---\left(8\right)$

　　为了找到超参数的优化值，对上述似然估计最大化得到超参数的更新公式：

　　$a_i=\frac{{\gamma }_i}{u_i},{\sigma }^2=\frac{{\left|\right|t-\mathrm{\Phi u}\left|\right|}^2}{N-{\Sigma }_{i=1}^N{\gamma }_i}---\left(9\right)$

　　式中γi=1-αiΣii

　　传统高斯核函数核参数均匀统一，限制了rvm模型的灵活性和预测精度; 基于提高预测精度的考虑，且不破坏其它性能，提出使用如下多高斯核函数：

　　$k(x_m,x_n)=\exp (-\underset{k=1}{\overset{d}{\Sigma }}{\eta }_k{(x_{\mathrm{mk}}-x_{\mathrm{nk}})}^2)$

　　其各个尺度上使用不同核参数，ηk是第k个核参数的平方的倒数，d是输入向 量的属性个数，则多尺度核参数可表示为：η=(η1,η2,...ηd);用 φnm=k(xm,xn)来表示贝叶斯矩阵的元素，则似然估计对第k个核参数的梯 度为：

　　$\frac{{\∂}_L}{{\∂}_{{\eta }_k}}=\underset{n=1}{\overset{N}{\Sigma }}\underset{m=1}{\overset{N}{\Sigma }}\frac{{\∂}_L}{{\∂}_{{\phi }_{\mathrm{nm}}}}\frac{{\∂}_{{\phi }_{\mathrm{nm}}}}{{\∂}_{{\eta }_k}}$

　　该式的第一部分与贝叶斯核参数无关，用来表示，得到矩阵：

　　D=(C-1ttTC-1-C-1)ΦA-1

　　=β[(t-y)uT-ΦΣ] (10)

　　似然估计对核参数求导为：$\frac{{\∂}_L}{{\∂}_{{\eta }_k}}=\underset{m=1}{\overset{N}{\Sigma }}\underset{n=1}{\overset{N}{\Sigma }}-D_{\mathrm{nm}}{\Phi }_{\mathrm{nm}}{(x_{\mathrm{mk}}-x_{\mathrm{nk}})}^2$

　　3)多高斯核函数核参数自优化算法

　　为了避免核参数过大或过小引起过平滑和过适应问题，增加限制条件从而 避免出现上述问题：

　　$\underset{k=1}{\overset{d}{\Sigma }}\log {\eta }_k=d\log \frac{1}{h^2}$

　　h是核参数几何平均值，则似然估计模型变成：

　　$L^{-}=\log p\left(t\right|\alpha ,\beta )=-\frac{1}{2}(N\log \left(2\pi \right)+\log |C|+t^T{C}^{-1}t)+\lambda (\underset{k=1}{\overset{d}{\Sigma }}\log {\eta }_k-d\log \frac{1}{h^2})---\left(11\right)$该模型 对核参数求导为：

　　$\frac{\∂L^{-}}{\∂{\eta }_k}=\frac{\∂L}{\∂{\eta }_k}+\frac{\lambda }{{\eta }_k},k=1,...,d$

　　$\frac{\∂L^{-}}{\∂{\eta }_k}=\underset{m=1}{\overset{N}{\Sigma }}\underset{n=1}{\overset{N}{\Sigma }}-D_{\mathrm{nm}}{\Phi }_{\mathrm{nm}}{(x_{\mathrm{mk}}-x_{\mathrm{nk}})}^2+\frac{\lambda }{{\eta }_k},k=1,...,d$

　　当上式第一部分对核参数求导时，所得梯度同号，为了保证所得核参数均大于 零且最大似然估计尽可能的大，可用如下公式更新核参数，

　　若不满足同号，为了保证核参数均大于零，且最大似然估计尽可能的大，梯度 小于零的核参数其更新公式为：

　　ηinew=p kηi (13)

　　梯度大于零的核参数其更新公式为：

　　式中i表示梯度小于零的属性列，j表示梯度大于零的属性列，p表示大于零的 梯度个数;

　　4)遗传优化算法对初始参数寻优模块

　　在建模过程中，多高斯核函数自优化相关向量机模型有两类参数，一类属 于核函数参数，核参数的个数由输入属性个数决定，核参数可通过上述算法中 介绍的自优化方法来确定;另一类是相关向量机模型的初始参数，多高斯核函 数自优化相关向量机的初始参数包括核参数几何平均值h和pk，其中核参数几 何平均值决定初始核参数的值，pk影响核参数的自优化过程;提出采用遗传优 化算法，对多高斯核函数自优化相关向量机模型中的初始参数h,pk进行优化， 具体优化算法的流程如下：

　　4.1)设定种群规模，遗传进化代数，染色体采用二进制编码，每个算子由 两段编码组成，两段编码分别代表两个参数h,pk，并确定各参数取值范围，生 成初始种群;

　　4.2)用初始种群训练多高斯核函数自优化相关向量机模型，目标函数取测 试样本的均方根误差函数RMSE;

　　4.3)个体进行选择、重组、变异，终止条件若达到最大进化数，则停止进 化，输出优化参数，否则继续寻优;

　　5)多高斯核函数自优化相关向量机软测量模型建模

　　污水处理中与BOD出水水质息息相关的输入属性为可降解固体浓度 RD-SED-G，悬浮固体浓度RD-SS-G，生化需氧量RD-DBO-G，化学需氧量 RD-DQO-G，初沉池中的生化需氧量RD-DBO-P，悬浮固体浓度RD-SS-P，二沉 池中的生化需氧量RD-DBO-S，化学需氧量RD-DQO-S，入水中的生化需氧量 DBO，化学需氧量DQO，二级处理中的化学需氧量DQO，生化需氧量DBO， 悬浮固体浓度SS，PH值PH-S，可降解固体浓度SED，出水的化学需氧量DQO-S， 可降解固体浓度SED-S，悬浮固体浓度SS-S，PH值PH-S;输入xn∈RM，是第n个输入值，tn是BOD的输出值，则出水BOD的预测算法步骤如 下：

　　5.1)对上述输入属性的污水数据进行归一化，去误差平滑处理，然后确定 训练数据和测试数据;

　　5.2)根据训练样本中的污水数据建立初始化模型，初始化模型参数: α=[1/N2,1/N2,...,1/N2]T，σ2=0.1var(t)，初始核参数η=[1/h2,1/h2,...,1/h2]T;

　　5.3)循环迭代

　　5.3.1)按上式(6),(7)更新u,Σ;

　　5.3.2)按上式(9)更新超参数α,β;

　　5.3.3)如果超参数αi大于给定的大值，则认为该超参数趋于无穷，从而将相 应的权值行设为零，并且忽略相应的贝叶斯矩阵列;否则，训练数据的相应训 练样本则为相关向量;

　　5.3.4)如果最大似然估计值变大，连续两代间的核参数最大变化值大于一 定的小值，则按上面公式(12)，(13)，(14)更新核参数η，并更新贝叶斯矩阵Φ， 否则停止更新;

　　5.3.5)如果连续两代间的超参数α最大变化值小于给定的小值，则迭代结束;

　　5.4)输出模型权值w，核参数η，相关向量机，噪声方差σ2。

　　说明书

　　基于多高斯核自优化相关向量机的污水水质软测量方法

　　技术领域

　　本发明涉及软测量的技术领域，尤其是指一种基于多高斯核自优化相关向 量机的污水水质软测量方法。

　　背景技术

　　随着全球经济的增长和人们生活水平的提高，城市生活污水和工业污水的 排放量日益增大，有限水资源受到不同程度的污染，防止水污染保护人们赖以 生存的水环境是人类面临的当务之急。保护水资源的一个重要方面就是要提高 污水处理的技术水平和检测手段。污水处理过程相当复杂，具有参数时变，多 变量耦合、强非线性，严重滞后等特点。使得出水水质不易在线测量，废水处 理成本高。污水处理过程中一些自动化检测设备、仪表的功能还不完善，处理 周期太长，远远达不到国家对环境保护的要求。同时国家对环境保护的投入加 大，污水处理技术越来越受到更多的关注。国家发展规划中明确提出要研发并 推广低能耗、有效的污水处理技术。解决污水生物处理过程中参数在线测量的 方法有两种：一是改进测量仪表，二是深入研究软测量技术，这对于出水的优 化排放有着重大的实际意义和应用价值。由于在线仪表设备投资大，维护困难 以及分析周期长、准确性不高，而软仪表成本低廉，测量具有实时性，尽管IAWQ 推出ASMs和ADM1等机理模型，但实际的污水处理现场条件太多，过程太复 杂，很难建立精确的机理模型，而神经网络、支持向量机等非机理建模都存在 局限性。相关向量机具有解更稀疏、核函数选择更自由，泛化能力更强，鲁棒 性更好等优点，使其在污水领域的应用中越来越受重视。但是传统高斯核函数 核参数均匀统一，限制了rvm模型的灵活性和预测精度。

　　污水排放标准中，衡量是否达标的参数指标有：化学需氧量COD、生化需 氧量BOD、氨氮、磷、固体悬浮物等。其中生化需氧量BOD和化学需氧量COD 反映水被有机污染的程序，BOD/COD的比率反映出了污水的生物降解能力。这 两个参数的测量对控制污水处理具有非常重要的价值。化学需氧量COD是指， 水样在一定条件下，以氧化1升水样中还原性物质所消耗的氧化剂的量为指标， 折算成每升水样全部被氧化后，需要的氧的毫克数，以mg/L表示。生化需氧量 BOD是指微生物在一定的温度和时间条件下分解氧化有机物所消耗的溶解氧 量，以mg/L表示。

　　现在的污水处理一般都采用稀释法、传感器等测量污水中BOD、COD的浓 度，但由于分析测定这两个指标的周期较长，测量中时常出现误差，不能及时 反应污水处理的现场情况，因而污水控制系统存在着较大的延时，不能发挥其 最佳的性能。

　　软测量技术就是利用易测量过程变量，依据这些易测量的过程变量和难以 直接测量的待测过程变量之间的数学模型，通过各种数学计算和估计方法，用 计算机软件实现待测量过程变量的测量。是近年在过程控制和检测领域涌现的 一种新技术。软测量作为现代复杂过程工业中较难甚至无法由硬件在线检测参 量实时估计的有效手段，具有投资低、维护保养简单等优点。将软测量技术用 于污水处理过程，能降低污水处理厂的能耗，节约成本，避免污水处理过程中 严重滞后等不足。但是污水过程非常复杂，传统的机理建模无法适应，而神经 网络、支持向量机等非机理建模都存在局限性，本发明提出多高斯核函数自优 化相关向量机模型，打破了传统高斯核函数参数均匀统一对预测精度的限制， 使模型更灵活。在保证模型收敛性和稀疏性的情况下，有效提高污水中BOD输 出精度。该模型是对基本rvm的改进，不仅离线情况下获得良好效果，在此基 础上展开基于多尺度高斯核自优化相关向量机的污水出水在线软测量研究也很 有意义。

　　发明内容

　　本发明的目的在于克服现有技术的不足，提供一种基于多高斯核自优化相 关向量机的污水水质软测量方法，通过自优化方法确定各尺度上的核参数，运 用遗传优化算法对初始参数寻优，建立最优模型。在保证模型收敛性和稀疏性 的情况下，有效提高污水中BOD输出精度。

　　为实现上述目的，本发明所提供的技术方案为：基于多高斯核自优化相关 向量机的污水水质软测量方法，包括以下步骤：

　　1)剔除污水输入和输出的数据中的异常点，由于各输入变量量纲的不同， 对其进行归一化处理，归一化到[0,1]区间中;

　　2)多高斯核函数相关向量机软测量模型模块，其计算公式：

　　给定一组输入和目标值xn∈RM，且考虑目标函数只 是一个标量，根据概率方程式，假设目标函数是模型的样本并且带有附加噪声：

　　tn=y(xn,w)+εn (1)

　　式中εn为附加噪声，服从(0,σ2)的高斯分布，且彼此间相互独立，因此 p(tn|y(xn),σ2)服从高斯分布，其分布由期望y(xn)和方差σ2决定，其中y(xn) 可由核函数的加权模型表示：

　　$y(x,w)=\underset{i=1}{\overset{N}{\Sigma }}{w}_{i}k(x,x_i)+w_0---\left(2\right)$

　　wi为模型权值，w=[w0,w1,w2,...,wn]T为(N+1)维列向量;k是核函数， φi=k(x,xi);t=[t1,t2,...tn]T为N维列向量，假设tn服从独立分布，数据集的 似然估计概率为：

　　$p\left(t\right|w,{\sigma }^2)={\left(2\pi {\sigma }^2\right)}^{-N/2}\exp \{-\frac{1}{2{\sigma }^2}{\left|\right|t-\mathrm{\Phi w}\left|\right|}^2\}---\left(3\right)$

　　φ(xn)=[1,k(xn,x1),k(xn,x2),...k(xn,xn)]T为(N+1)*1维矩阵，贝叶斯矩阵表示 为：Φ=[φ(x1),φ(x2),...,φ(xn)]T，其是N*(N+1)维;为了约束rvm模型中 权值w，假设其服从(0,αi-1)高斯分布，且设各权值间相互独立，其先验概率表 示如下：

　　$p\left(w\right|\alpha )=\underset{i=0}{\overset{N}{\Pi }}N\left(w_i\right|0,{{\alpha }_i}^{-1})---\left(4\right)$

　　α为N+1维超参数，引入超参数导致算法的稀疏性;

　　根据贝叶斯准则，可得到后验概率公式：

　　给定新的测试样本x，预测相应的目标t*，按照预测分布：

　　$p\left(t_{*}\right|t)=\∫p\left(t_{*}\right|w,\alpha ,{\sigma }^2)p(w,\alpha ,{\sigma }^2|t)d_w{d}_{\alpha }{d}_{{\sigma }^2}$

　　无法计算后验概率，因为无法计算$p\left(t\right)=\∫p\left(t\right|w,\alpha ,{\sigma }^2)p(w,\alpha ,{\sigma }^2|t)d_w{d}_{\alpha }{d}_{{\sigma }^2}$

　　所以将后验概率分解：p(w,α,σ2|t)=p(w|t,α,σ2)p(α,σ2|t)

　　可得权重的后验概率为：

　　$\begin{array}{c}p\left(w\right|t,\alpha ,{\sigma }^2)=\frac{p\left(t\right|w,{\sigma }^2)p\left(w\right|\alpha )}{p\left(t\right|\alpha ,{\sigma }^2)}\\ ={\left(2\pi \right)}^{-(N+1)/2}{\left|\Sigma \right|}^{-1/2}\exp \{-\frac{1}{2}{(w-u)}^T{\Sigma }^{-1}(w-u)\}\end{array}---\left(5\right)$

　　其后验协方差和均值分别为：

　　Σ=(σ-2ΦTΦ+A)-1 (6)

　　u=σ-2ΣΦTt (7)

　　因为p(α,σ2|t)∝p(t|α,σ2)p(α)p(σ2)，所以可以用后者等价前者：

　　$\begin{array}{c}p(t,a,{\sigma }^2)=\∫p\left(t\right|w,\beta )p\left(w\right|\alpha )d_w\\ ={\left(2\pi \right)}^{-N/2}{|{\sigma }^{2}I+\Phi A^{-1}{\Phi }^T|}^{-1/2}\exp (-\frac{1}{2}{t}^T\mathrm{Ct})\end{array}$

　　其中矩阵C=(σ2I+ΦA-1ΦT)-1，对上述式子取对数得：

　　$L=\log p\left(t\right|\alpha ,\beta )=-\frac{1}{2}(N\log \left(2\pi \right)+\log |C|+t^T{C}^{-1}t)---\left(8\right)$

　　为了找到超参数的优化值，我们对上述似然估计最大化得到超参数的更新公式：

　　$a_i=\frac{{\gamma }_i}{u_i},{\sigma }^2=\frac{{\left|\right|t-\mathrm{\Phi u}\left|\right|}^2}{N-{\Sigma }_{i=1}^N{\gamma }_i}---\left(9\right)$

　　式中γi=1-αiΣii

　　相较于线性核函数，多项式核函数，sigmoid核函数，高斯核函数使用得更 多;传统高斯核函数核参数均匀统一，限制了rvm模型的灵活性和预测精度; 基于提高预测精度的考虑，且不破坏其它性能，提出使用如下多高斯核函数：

　　$k(x_m,x_n)=\exp (-\underset{k=1}{\overset{d}{\Sigma }}{\eta }_k{(x_{\mathrm{mk}}-x_{\mathrm{nk}})}^2)$

　　其各个尺度上使用不同核参数，ηk是第k个核参数的平方的倒数，d是输入向 量的属性个数，则多尺度核参数可表示为：η=(η1,η2,...ηd);用 φnm=k(xm,xn)来表示贝叶斯矩阵的元素，则似然估计对第k个核参数的梯 度为：

　　$\frac{{\∂}_L}{{\∂}_{{\eta }_k}}=\underset{n=1}{\overset{N}{\Sigma }}\underset{m=1}{\overset{N}{\Sigma }}\frac{{\∂}_L}{{\∂}_{{\phi }_{\mathrm{nm}}}}\frac{{\∂}_{{\phi }_{\mathrm{nm}}}}{{\∂}_{{\eta }_k}}$

　　该式的第一部分与贝叶斯核参数无关，用来表示，得到矩阵：

　　D=(C-1ttTC-1-C-1)ΦA-1

　　=β[(t-y)uT-ΦΣ] (10)

　　似然估计对核参数求导为：$\frac{{\∂}_L}{{\∂}_{{\eta }_k}}=\underset{m=1}{\overset{N}{\Sigma }}\underset{n=1}{\overset{N}{\Sigma }}-D_{\mathrm{nm}}{\Phi }_{\mathrm{nm}}{(x_{\mathrm{mk}}-x_{\mathrm{nk}})}^2$

　　3)多高斯核函数核参数自优化算法

　　为了避免核参数过大或过小引起过平滑和过适应问题，增加限制条件从而 避免出现上述问题：

　　$\underset{k=1}{\overset{d}{\Sigma }}\log {\eta }_k=d\log \frac{1}{h^2}$

　　h是核参数几何平均值，则似然估计模型变成：

　　$L^{-}=\log p\left(t\right|\alpha ,\beta )=-\frac{1}{2}(N\log \left(2\pi \right)+\log |C|+t^T{C}^{-1}t)+\lambda (\underset{k=1}{\overset{d}{\Sigma }}\log {\eta }_k-d\log \frac{1}{h^2})---\left(11\right)$该模型 对核参数求导为：

　　$\frac{\∂L^{-}}{\∂{\eta }_k}=\frac{\∂L}{\∂{\eta }_k}+\frac{\lambda }{{\eta }_k},k=1,...,d$

　　$\frac{\∂L^{-}}{\∂{\eta }_k}=\underset{m=1}{\overset{N}{\Sigma }}\underset{n=1}{\overset{N}{\Sigma }}-D_{\mathrm{nm}}{\Phi }_{\mathrm{nm}}{(x_{\mathrm{mk}}-x_{\mathrm{nk}})}^2+\frac{\lambda }{{\eta }_k}k=1,...,d$

　　当上式第一部分对核参数求导时，所得梯度同号，为了保证所得核参数均大于 零且最大似然估计尽可能的大，可用如下公式更新核参数，

　　若不满足同号，为了保证核参数均大于零，且最大似然估计尽可能的大，梯度 小于零的核参数其更新公式为：

　　ηinew=p kηi (13)

　　梯度大于零的核参数其更新公式为：

　　式中i表示梯度小于零的属性列，j表示梯度大于零的属性列，p表示大于零的 梯度个数;

　　4)遗传优化算法对初始参数寻优模块

　　在建模过程中，多高斯核函数自优化相关向量机模型有两类参数，一类属 于核函数参数，核参数的个数由输入属性个数决定，核参数可通过上述算法中 介绍的自优化方法来确定;另一类是相关向量机模型的初始参数，多高斯核函 数自优化相关向量机的初始参数包括核参数几何平均值h和pk，其中核参数几 何平均值决定初始核参数的值，pk影响核参数的自优化过程;提出采用遗传优 化算法，对多高斯核函数自优化相关向量机模型中的初始参数h,pk进行优化， 具体优化算法的流程如下：

　　4.1)设定种群规模，遗传进化代数，染色体采用二进制编码，每个算子由 两段编码组成，两段编码分别代表两个参数h,pk，并确定各参数取值范围，生 成初始种群;

　　4.2)用初始种群训练多高斯核函数自优化相关向量机模型，目标函数取测 试样本的均方根误差函数RMSE;

　　4.3)个体进行选择、重组、变异，终止条件若达到最大进化数，则停止进 化，输出优化参数，否则继续寻优;

　　5)多高斯核函数自优化相关向量机软测量模型建模

　　污水处理中与BOD出水水质息息相关的输入属性为可降解固体浓度 RD-SED-G，悬浮固体浓度RD-SS-G，生化需氧量RD-DBO-G，化学需氧量 RD-DQO-G，初沉池中的生化需氧量RD-DBO-P，悬浮固体浓度RD-SS-P，二沉 池中的生化需氧量RD-DBO-S，化学需氧量RD-DQO-S，入水中的生化需氧量 DBO，化学需氧量DQO，二级处理中的化学需氧量DQO，生化需氧量DBO， 悬浮固体浓度SS，PH值PH-S，可降解固体浓度SED，出水的化学需氧量DQO-S， 可降解固体浓度SED-S，悬浮固体浓度SS-S，PH值PH-S;输入xn∈RM，是第n个输入值，tn是BOD的输出值，则出水BOD的预测算法步骤如 下：

　　5.1)对上述输入属性的污水数据进行归一化，去误差平滑处理，然后确定 训练数据和测试数据;

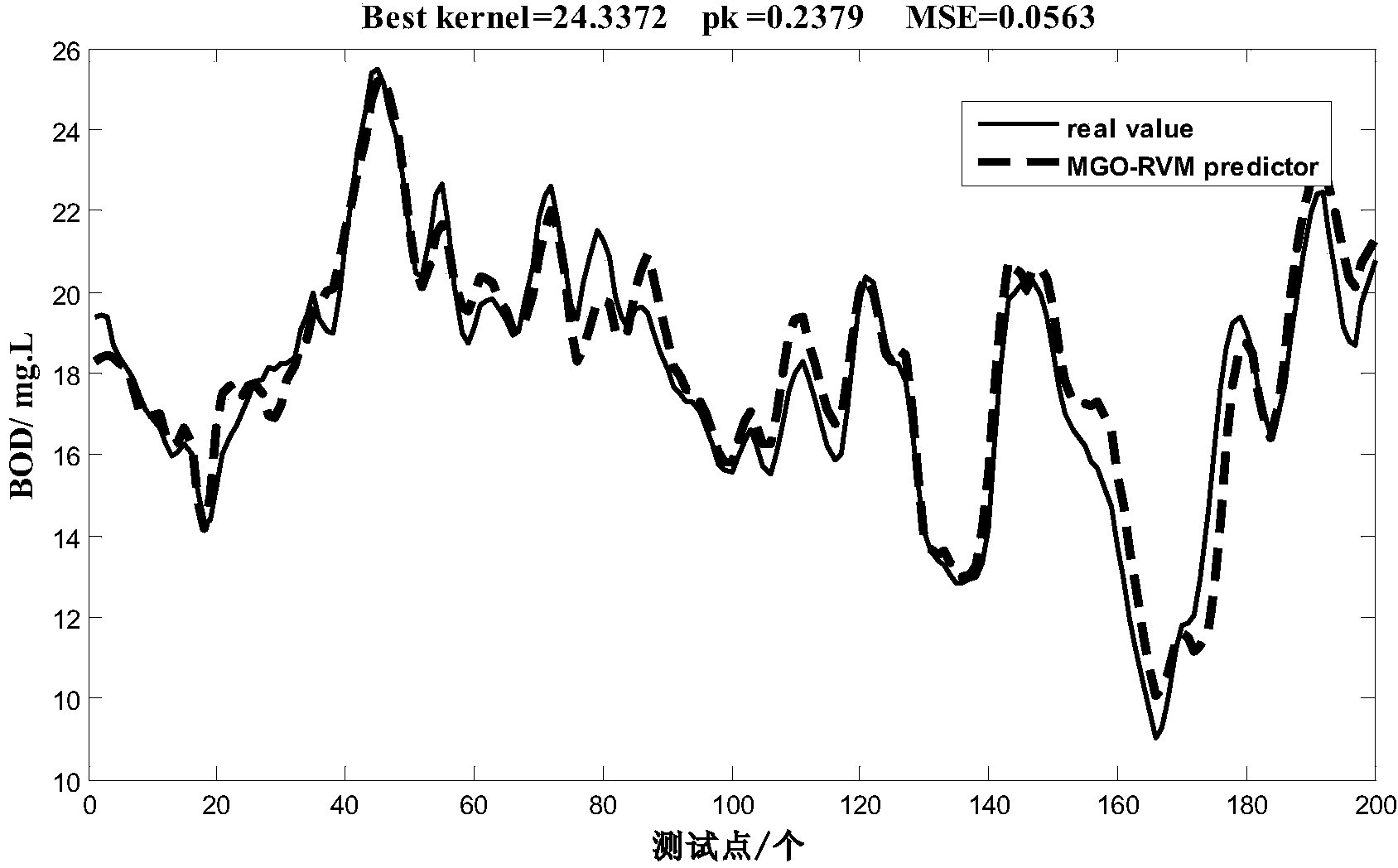
　　5.2)根据训练样本中的污水数据建立初始化模型，初始化模型参数: α=[1/N2,1/N2,...,1/N2]T，σ2=0.1var(t)，采用上面提到的遗传优化算法得到最佳 初始核参数几何平均值h=24.3372,pk=0.2379,初始核参数η=[1/h2,1/h2,...,1/h2]T;

　　5.3)循环迭代

　　5.3.1)按上式(6),(7)更新u,Σ;

　　5.3.2)按上式(9)更新超参数α,β;

　　5.3.3)如果超参数αi大于给定的大值，则认为该超参数趋于无穷，从而将相 应的权值行设为零，并且忽略相应的贝叶斯矩阵列;否则，训练数据的相应训 练样本则为相关向量;

　　5.3.4)如果最大似然估计值变大，连续两代间的核参数最大变化值大于一 定的小值，则按上面公式(12)，(13)，(14)更新核参数η，并更新贝叶斯矩阵Φ， 否则停止更新;

　　5.3.5)如果连续两代间的超参数α最大变化值小于给定的小值，则迭代结束;

　　5.4)输出模型权值w，核参数η，相关向量机，噪声方差σ2。

　　本发明与现有技术相比，具有如下优点与有益效果：

　　1、本发明建立了一种基于多高斯核函数自优化相关向量机的软测量模型， 模型通过自优化方法确定各尺度上的核参数，同时运用遗传优化算法对初始参 数寻优，建立最优模型，在保证模型收敛性和稀疏性的情况下，有效提高污水 中BOD输出精度，该模型是对基本rvm的改进，不仅离线情况下获得良好效果， 在此基础上展开基于多尺度高斯核自优化相关向量机的污水出水在线软测量研 究也很有意义。

　　2、本发明的核函数由多个高斯函数组成，具有多尺度核参数，打破了传统 高斯核函数参数均匀统一对预测精度的限制，使模型更灵活。

相关推荐

©中国污水处理工程网 版权所有
访问电脑版