污水处理出水参数预测方法

　　申请日2017.03.17

　　公开(公告)日2017.07.28

　　IPC分类号G06Q10/04; G06N3/02

　　摘要

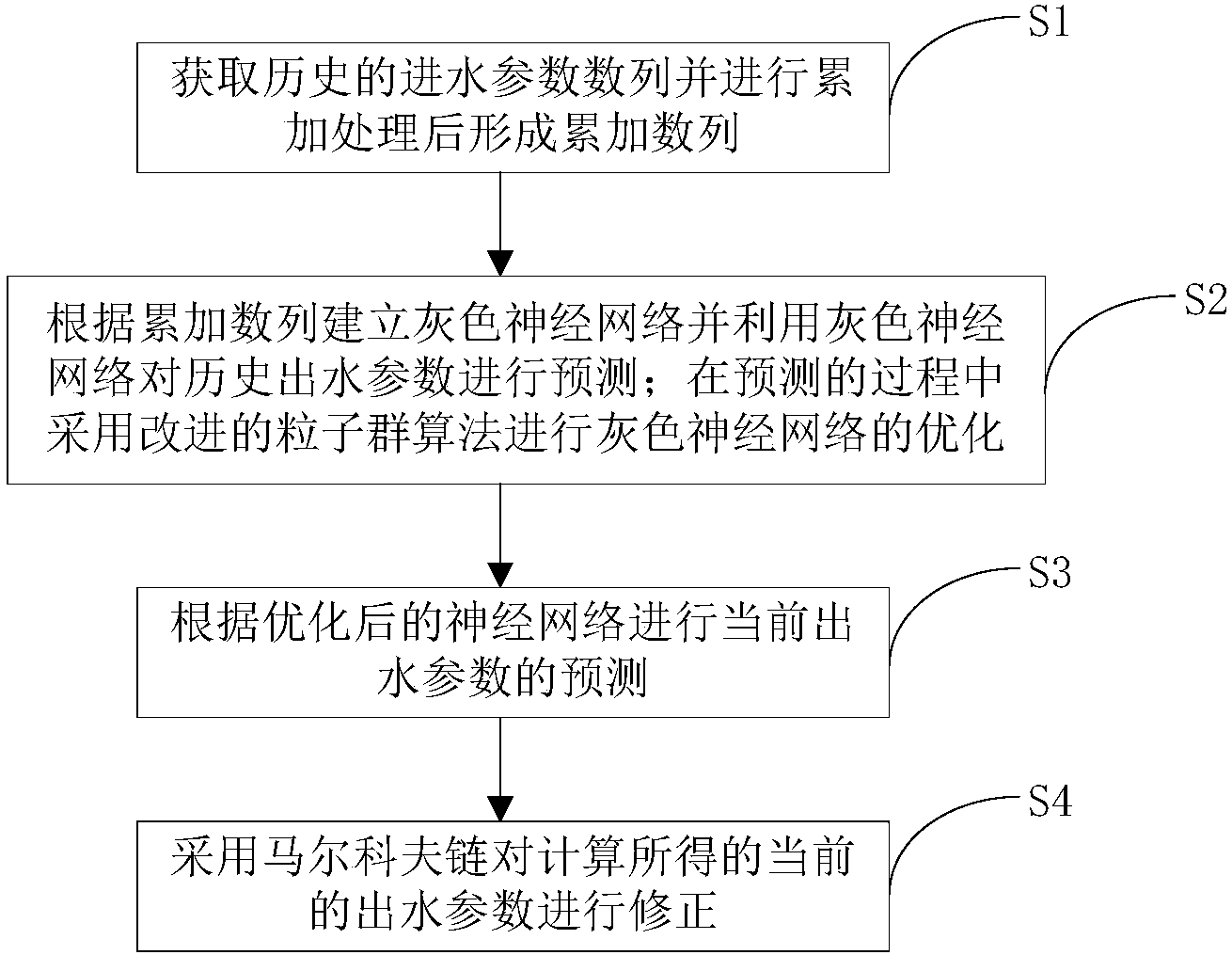
　　本发明提供一种基于灰色神经网络组合模型的污水处理出水参数预测方法，该方法包括：获取历史的进水参数数列x(t)并进行累加处理后形成累加数列y(t);根据累加数列y(t)建立灰色神经网络并利用灰色神经网络对历史出水参数进行预测，在预测的过程中采用改进的粒子群算法进行灰色神经网络的优化;根据优化后的神经网络进行当前出水参数的预测;采用马尔科夫链对计算所得的当前的出水参数进行修正。

　　摘要附图

　　权利要求书

　　1.一种基于灰色神经网络组合模型的污水处理出水参数预测方法，其特征在于，包括：

　　获取历史的进水参数数列x(t)并进行累加处理后形成累加数列y(t);

　　根据累加数列y(t)建立灰色神经网络并利用灰色神经网络对历史出水参数进行预测;在预测的过程中采用改进的粒子群算法进行灰色神经网络的优化，优化的步骤如下：

　　步骤一，初始化改进的粒子群算法内的参数;

　　步骤二，计算每个离子的粒子的适应度f：

　　 $f = \frac{1}{n} Σ_{i = 1}^{n} Σ_{j = 1}^{m} | y_{i j} - t_{i j} | - - - (1)$

　　其中，yij为测试样本总群X的预测值;tij为测试样本总群X的真实值;n为测试样本的个数;m为输出节点的个数;

　　步骤三，根据计算的适应度f，找出最小适应度fmin对应的粒子个体Xmin，令X*=Xmin，f*=fmin，则X*为最优粒子，f*为最优适应度;

　　步骤四，按照以下公式优化每个粒子的位置Xi和速度Vi;

　　 $v_{i d}^{k + 1} = {ωv}_{i d}^{k} + c_{1} r_{1} (p_{i d}^{k} - x_{i d}^{k}) + c_{2} r_{2} (g_{d}^{k} - x_{i d}^{k}) - - - (2)$

　　 $x_{i d}^{k + 1} = x_{i d}^{k} + v_{i d}^{k + 1} - - - (3)$

　　样本种群X=(X1，X2，…，Xn);其中粒子i的位置信息表示为Xi=(xi1，xi2，…，xid)T;速度信息表示为Vi=(vi1，vi2，…，vid)T;粒子i的个体极值点为Pi=(pi1，pi2，…，pid)T;种群的全局极值点为G=(g1，g2，…，gd)T;表示粒子i在第k次迭代第d维的速度;c1，c2为加速系数;r1，r2为[0,1]之间的随机数;ω为惯性因子;为第k次迭代第d维的全局极值点;

　　步骤五，以变异遗传概率P对粒子Xi的位置进行更新，产生新的粒子Xi′并线性递减惯性权重，计算新的粒子Xi′的适应度f′;比较f和f′的大小，若f>f′，则令Xi=Xi′;

　　步骤六，对于更新后的种群，找出最小的fmin，及其对应的Xmin，若fmin

　　步骤七，重复步骤四至步骤六，当迭代次数达到最大值时结束循环，输出f*，X*;把X*的值赋给参数a，bi，实现灰色神经网络的优化;

　　根据优化后的神经网络进行当前出水参数的预测;

　　采用马尔科夫链对计算所得的当前的出水参数进行修正。

　　2.根据权利要求1所述的基于灰色神经网络组合模型的污水处理出水参数预测方法，其特征在于，根据累加数列建立灰色神经网络并利用灰色神经网络对历史出水参数进行预测的步骤如下：

　　根据累加数列y(t)构建灰色神经网络的微分方程：

　　 $\frac{{dy}_{1}}{d t} + {ay}_{1} = b_{1} y_{2} + b_{2} y_{3} + ... + b_{n - 1} y_{n} - - - (3)$

　　求解微分方程后得到其时间响应函数：

　　 $\begin{matrix} z (t) = (y_{1} (0) - d) e^{- a t} + d \\ = ((y_{1} (0) - d) - y_{1} (0) * \frac{1}{1 + e^{- a t}} + 2 d * \frac{1}{1 + e^{- a t}}) * (1 + e^{- a t}) \end{matrix} - - - (4)$

　　其中：z(t)为对出水参数的预测值;

　　将时间响应函数内的参数映射到BP神经网络内相应层的权重上，得到灰色神经网络;

　　在累加数列y(t)获取测试样本对灰色神经网络进行训练，当网络收敛时提取a，b1，b2，…，bn-1这些时间响应函数内的参数，将时间响应函数进行白化;

　　利用白化后的时间响应函数对历史出水参数进行预测。

　　3.根据权利要求2所述的基于灰色神经网络组合模型的污水处理出水参数预测方法，其特征在于，BP神经网络内相应层的权重的赋值如下：

　　输入变量的权重w11=a，输入层与隐含层的权重i=2,3,…,n，隐含层与输出层的权重w3i=1+e-at，j=1,…,n;灰色神经网络输出公式：

　　y1=w31c1+w32c2+…+w3ncn-θy1 (5)

　　其中：c1=hw21，ci=yi(t)hw2i，i=2,…,n，θy1=(1+e-at)(d-y1(0))。

　　4.根据权利要求1所述的基于灰色神经网络组合模型的污水处理出水参数预测方法，其特征在于，采用以下公式以变异遗传概率P对粒子Xi的位置进行更新：

　　 $x_{i j} = \{\begin{matrix} x_{i j} + (x_{i j} - a_{\max}) f (k) & r &GreaterEqual; 05 \\ x_{i j} + (a_{\min} - x_{i j}) f (k) & r < 0.5 \end{matrix} - - - (6)$

　　其中，xij表示第i个粒子的第j个方向的位置信息;f(k)=r(1-k/Kmax)，k表示当前迭代次数，Kmax表示最大迭代次数;amax，amin分别为xij的上界和下界，r为[0,1]之间的随机数;

　　采用以下公式线性递减惯性权重：

　　ω(k)=ωs-(ωs-ωe)(Kmax-k)/Kmax (7)

　　其中，ωs为初始惯性权重;ωe为最终迭代惯性权重，ω(k)为第k次迭代时的惯性权重。

　　5.根据权利要求1所述的基于灰色神经网络组合模型的污水处理出水参数预测方法，其特征在于，采用马尔科夫链对计算所得的当前的出水参数进行修正的步骤如下：

　　采用预测结果相对误差的绝对值，将预测值序列分为若干个状态区间，求得一步转移概率矩阵其中为一步转移概率，表示从状态ai经过一步转移到状态aj的概率，采用以下公式进行修正：

　　Pt=P0[P(1)]t (8)

　　Pt为t时刻预测值的概率分布;P0为初始时刻预测值的概率分布。

　　说明书

　　基于灰色神经网络组合模型的污水处理出水参数预测方法

　　技术领域

　　本发明涉及污水处理领域，且特别涉及一种基于灰色神经网络组合模型的污水处理出水参数预测方法。

　　背景技术

　　污水处理是控制水污染的关键一环。由于相关污水监控设备价格昂贵，因此部分中小污水处理厂出于成本问题或出水监测设备维护困难等问题，存在相关参数监控不理想情况。然而一些参数的不精确不仅对出水水质有重要影响，同时也增加了污水处理成本。

　　目前，对污水处理厂水质预测的方法有很多，但是大都是基于神经网络的预测。污水处理厂水质的变化是有多种影响因素构成的，单一的预测方法仅能对局部的变化规律进行描述，因而预测精度不高。因此，改进单一模型的预测方法便成了提高预测精度的重要手段。

　　发明内容

　　本发明为了克服现有单一性预测方法预测准确性低的问题，提供一种预测精度高的基于灰色神经网络组合模型的污水处理出水参数预测方法。

　　为了实现上述目的，本发明提供一种基于灰色神经网络组合模型的污水处理出水参数预测方法，该方法包括：

　　获取历史的进水参数数列x(t)并进行累加处理后形成累加数列y(t);

　　步骤一，初始化改进的粒子群算法内的参数;

　　步骤二，计算每个离子的粒子的适应度f：

　　其中，yij为测试样本总群X的预测值;tij为测试样本总群X的真实值;n为测试样本的个数;m为输出节点的个数;

　　步骤三，根据计算的适应度f，找出最小适应度fmin对应的粒子个体Xmin，令X*=Xmin，f*=fmin，则X*为最优粒子，f*为最优适应度;

　　步骤四，按照以下公式优化每个粒子的位置Xi和速度Vi;

　　步骤六，对于更新后的种群，找出最小的fmin，及其对应的Xmin，若fmin

　　步骤七，重复步骤四至步骤六，当迭代次数达到最大值时结束循环，输出f*，X*。把X*的值赋给参数a，bi，实现灰色神经网络的优化;

　　根据优化后的神经网络进行当前出水参数的预测;

　　采用马尔科夫链对计算所得的当前的出水参数进行修正。

　　于本发明一实施例中，根据累加数列建立灰色神经网络并利用灰色神经网络对历史出水参数进行预测的步骤如下：

　　根据累加数列y(t)构建灰色神经网络的微分方程：

　　求解微分方程后得到其时间响应函数：

　　其中：z(t)为对出水参数的预测值;

　　将时间响应函数内的参数映射到BP神经网络内相应层的权重上，得到灰色神经网络;

　　在累加数列y(t)获取测试样本对灰色神经网络进行训练，当网络收敛时提取a，b1，b2，…，bn-1这些时间响应函数内的参数，将时间响应函数进行白化;

　　利用白化后的时间响应函数对历史出水参数进行预测。

　　于本发明一实施例中，BP神经网络内相应层的权重的赋值如下：

　　输入变量的权重w11=a，输入层与隐含层的权重i=2,3,…,n，隐含层与输出层的权重w3i=1+e-at，j=1,…,n。灰色神经网络输出公式：

　　y1=w31c1+w32c2+…+w3ncn-θy1(5)

　　其中：c1=hw21，ci=yi(t)hw2i，i=2,…,n，θy1=(1+e-at)(d-y1(0))。

　　于本发明一实施例中，采用以下公式以变异遗传概率P对粒子Xi的位置进行更新：

　　采用以下公式线性递减惯性权重：

　　ω(k)=ωs-(ωs-ωe)(Kmax-k)/Kmax(7)

　　其中，ωs为初始惯性权重;ωe为最终迭代惯性权重，ω(k)为第k次迭代时的惯性权重。

　　于本发明一实施例中，采用马尔科夫链对计算所得的当前的出水参数进行修正的步骤如下：

　　Pt+1=P0[P(1)]t+1 (8)

　　Pt+1为t+1时刻预测值的概率分布;P0为初始时刻预测值的概率分布。

　　综上所述，本发明提供的基于灰色神经网络组合模型的污水处理出水参数预测方法利用改进的粒子群算法与灰色神经网络相融合，用改进粒子群算法优化灰色神经网络权值，利用灰色神经网络的输出的均方差作为粒子适应度，实现了模型参数的优化。再用马尔科夫链对误差进行修正，使得修正值更加接近实际值。多种算法的融合，综合利用各自算法的优点，提高了污水处理水质参数的预测精度，具有良好的扩展性和实际应用价值。

　　为让本发明的上述和其它目的、特征和优点能更明显易懂，下文特举较佳实施例，并配合附图，作详细说明如下。